خصائص المنحنى الطبيعي المعتدل

التوزيع المعتدل (الطبيعي) Normal Distribution
يرتبط هذا التوزيع بمتغير عشوائي متصل وهو دالة في المتغير العشوائي ويمكنتمثيله بيانياً وهو من أهم التوزيعات الاحتمالية لتمثيله العديد منالظواهر وهو المناسب لها سواء كانت القيم التي تحدث في الظاهرة كبيرة جداًأو صغيرة جداً باحتمالات صغيرة.
هو توزيع مستمر يعرف أيضاً بتوزيع جاوس (كارل جاوس) حيث جرى نشره سنة1733م ويعتبر المتغير المعتدل عشوائي مستمر لكونه يتكون من عدد لانهائي منالقيم الحقيقية والتي يمكن ترتيبها على مقياس متصل، وهو من أهم التوزيعاتفي علم الإحصاء بل يعتبر أساساً لكثير من النظريات الإحصائية الرياضيةويلعب دوراً أساسياً في اختبارات الفروض الإحصائية وفترات الثقة وغير ذلكوأن الكثير من الصفات كالطول والوزن ومستوى الذكاء والزواج وما إلى ذلكإذا قيست ولعدد كبير من المشاهدات فإن توزيعها يقترب من التوزيع الطبيعيإن لم يكن يأخذ صورة التوزيع الطبيعي، ويعرف بأسماء مختلفة منها التوزيعألجرسي لكون شكله يشبه ألجرس.

خصائص التوزيع المعتدل:
1) منحنى التوزيع المعتدل متصل (مستمر) منحناه (Normal Curve) يشبه شكل الجرس ويمتد ذراعه من – ∞ إلى ∞ .
معادلته الرياضية في الفترة ] – ∞ ، ∞ [ هي:

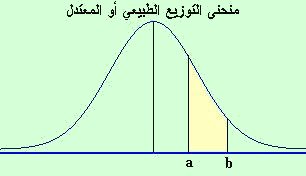
بإجراء تكامل Y على الفترة ] – ∞ ، ∞ [ نحصل على المساحة تحت المنحنى وفوق المحور الأفقي، والتمثيلالبياني له كما مبين بالشكل المقابل وكل نقطة من نقاط المنحنى تمثل قيمةلدالة تعرف بدالة كثافة الاحتمال (Probability density function) عند هذهالنقطة والاحتمال هنا أي في التوزيع المستمر هوقيمة المساحة تحت منحنى دالة الكثافة المناظرة لفترة وليس لنقطة فالمساحةباللون الأصفر والمحصورة بين المنحنى والمحور الأفقي والمستقيمان x1 = a ,x2 = b تساوي احتمال المتغير العشوائي المستمر X أي قيمة في الفترة [ a ,b] هذا وأن المساحة الكلية الواقعة بين منحى التوزيع المعتدل والخط الأفقيتساوي الواحد الصحيح وهي ما تعرف بالمساحة تحت المنحنى = 1 ولمعرفة احتمالوقوع x بين x1 و x2 نحسب تكامل الدالة السابقة من x1 إلى x2 ، مع ملاحظةأن احتمال أي حدث P(A)s يقع بين الصفر والواحد الصحيح أي أن: 1s>sP(A)s>s0
2) المنحنى متماثل حول الخط الرأسي (العمود النازل من أعلى نقطةللمنحنى على الخط الأفقي) وإن التماثل يعني بأن صورة الشكل على أحد جانبيمحور التماثل هي الجزء الواقع على الجانب الأخر وموقع العمود على الخطالأفقي يمثل قيمة الوسط الحسابي أي أن المنحنى متماثل حول وسطه الحسابي أوحول المستقيم x = μ ، وان μ هي
القيمة المتوقعة ويصل المنحنى لقيمته العظمى عند X = μ
3) المنحنى ممتد من – ∞ إلى + ∞ ولا يلتقي بالمحور الأفقي.
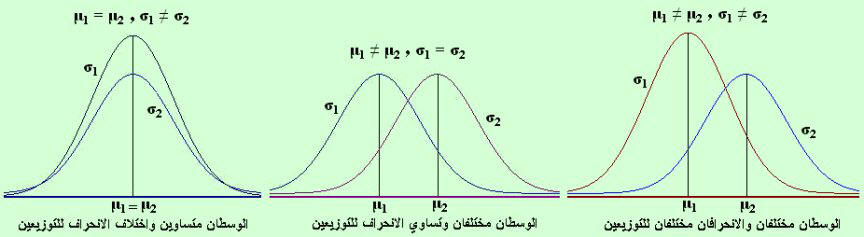
4) للمنحنى المعتدل معلمتين هما الوسطالحسابي والانحراف المعياري معتمد كلياً عليهم فاختلاف الوسط أو الانحرافالمعياري لتوزيعين معتدلين يعني اختلاف في الشكل أو
اختلاف في المركز كما مبين بالشكل الآتيولكل زوج ( μ ، σ ) للوسط والانحراف المعياري منحنى توزيع مختلف وبالتاليتختلف المساحة تحت المنحنى لكل منحنى ولذا
أخذنا ( 0 ، 1) كتوزيع معياري يسمى التوزيع الطبيعي المعياري متغيره العشوائي هو Z السابق ذكرها، وهنا جدول خاص بها.

هذه الصورة بحجم اخر انقر هنا لعرض الصورة بالشكل الصحيح ابعاد الصورة هي 864x237.

5) للمنحنى قمة واحدة أي له منوال واحد وبالتالي فالمنحني وحيد المنوال
6) المتوسطات الثلاثة متساوية (الوسط والوسيط والمنوال) بالنسبة للمتغير العشوائي المعتاد.
7) المساحة الواقعة تحت المنحنى والمحصورة بالمستقيمين:
x = μ – σ و x = μ + σ تساوي 68.26% تقريباً من المساحة الكلية تحت المنحنى أي 68.26% من قيم المتغير العشوائي المعتاد تقع في [μ + σ ، μ – σ]
x = μ – 2σ و x = μ + 2σ تساوي 95.45% تقريباً من المساحة الكلية تحت المنحنى أي 95.45% من قيم المتغير العشوائي المعتاد تقع في [μ + 2σ ، μ – 2σ]
x = μ – 3σ و x = μ + 3σ تساوي 99.73% تقريباً من المساحة الكلية تحت المنحنى أي 99.73% من قيم المتغير العشوائي المعتاد تقع في [μ + 2σ ، μ – 2σ]
أي أن وقوع أي مفردة على بعد 1، 2، 3 انحرافات معيارية (s1s, 2s, 3s) من الوسط الحسابي هي القيم السابقة كما مبين بالشكل الآتي:

لاحظ أن 34.19% من المساحة تحت المنحنى التي تساوي الواحد الصحيح أي0.3413 ، وبجمع القيم المبينة في الرسم أعلاه نجد أنها تساوي الواحدالصحيح تقريباً.
إن هذه القيم ما هي إلا احتمالات للقيم كمساحة تحت المنحنى ولأي دالةاحتمال يكون مجموع احتمالاتها البسيطة يساوي الواحد الصحيح ونقصد في الأصلالمساحة هنا لمساحة الأعمدة للقيم ولكن من الصعب رسم كل الأعمدة وعرضاحتمال كل منها ولذا استعضنا عنها باحتمالاتها.
0.0013 + 0.0214 + 0.1359 + 0.3413 + 0.3413 + 0.1359 + 0.0214 + 0.0013 = 0.9998 ≈ 1
والتوزيعالطبيعي المعياري (Standard Normal Distribution) الذي وسطه صفر وانحرافهالمعياري 1 متغيره العشوائي المعياري Z بالصيغة السابق ذكرها، ومنحناه كمامبين أعلاه ويمكن حذف s من القيم على الخط الأفقي وقد نضع قيم x والمناظرةلها Z على الخط الأفقي إن دعت الحاجة.
وقد أمكن إيجاد جدول لتوزيع معتدل معياري لقياس جميع التوزيعات المعتادة (اعتدالي) من خلال النظرية التالية:
إذا كانت x متغير عشوائي له توزيعاعتدالي بتوقع μ وتباين σ2 حيث σ الانحراف المعياري فإن: Z = (x – μ)÷σ لهتوزيع اعتدالي وسطه صفر وانحرافه المعياري واحد صحيح ويعرف بالتوزيعالمعتدل المعياري وله جداول لقيم دالة التوزيع الاحتمالي ولقيم دالة كثافةالاحتمال لأي قيمة من قيم المتغير العشوائي، ويعرف المنحنى هنا بالمنحنىالطبيعي القياسي خطه الأفقي مقسم لدرجات Z كما مبين بالشكل التالي والذييبين أيضاً المساحة تحت المنحنى وقد قسمت لدرجات معيارية حسب قيم Z حيثقيم x تناظرها قيم Z تحسب من الصيغة الرياضية السابقة أو من الصيغة: Z = (x –`X ) ÷ s حيث s الانحراف المعياري وأن القيمة Z قيمة معيارية وهي الفرق بين القيمةالمشاهدة والوسط الحسابي معبراً عنها بوحدات معيارية بمعنى أكثر دقة قيمةZ عبارة عن عدد الوحدات المعيارية (الانحراف المعياري) التي تفصل بين قيمةx والوسط الحسابي.
وهناك خواص أخرى من بينها إذا كان Ln(x)s توزيع طبيعي فإن x توزيع طبيعي وستذكر الأخرى في حينها والخاصة بتوزيع ذات الحدين وتوزيع χ2 .
يمكن صياغة معادلة المنحنى بدلالة Z على الصورة الآتية حيث أن Y تمثل كثافة قيم المتغير الطبيعي المعياري أو التكرارات للمنحنى.

يمكن تحويل قيمة المتغير المعتدل xلمتغير معتدل معياري Z من الصيغة السابقة فمثلاً إذا كان لدينا توزيعاعتدالي وسطه 150 درجة وانحرافه المعياري 90 درجة فيمكن باستخدام الصيغةالسابقة حساب قيمة x = 270 نستخدم الصيغة السابقة أي أن:
Z = ( 270 – 90) ÷ 90 = 2
بالرجوع لجدول Z نجد أن المساحة تحت المنحنى التي تقابل Z = 2 تساوي 0.9772 (المساحة التي تقع على يسار العدد 2 (الشكل كل السابق)، وتحسب بطريقتين:
الأولى : المساحة = 1 – (0.0013 + 0.0214) = 1 – 0.0227 = 0.9773
الثانية : المساحة = 0.0013 + 0.0214 + 0.1359 + 0.3413 + 0.3413 + 0.1359 =

» المنحني الطبيعي المعياري - بخصائصه معرب-